27、堆
思考:在实际的软件开发中,快速排序的性能要比堆排序好,这是为什么呢?
主要内容
什么是堆
堆是一种特殊的树,满足以下两点的就是堆:
1、完全二叉树(叶子节点都在最底下两层,最底层节点靠左排列,其他层节点数达最大)
2、父节点的值必须大于等于(或小于等于)其左右节点的值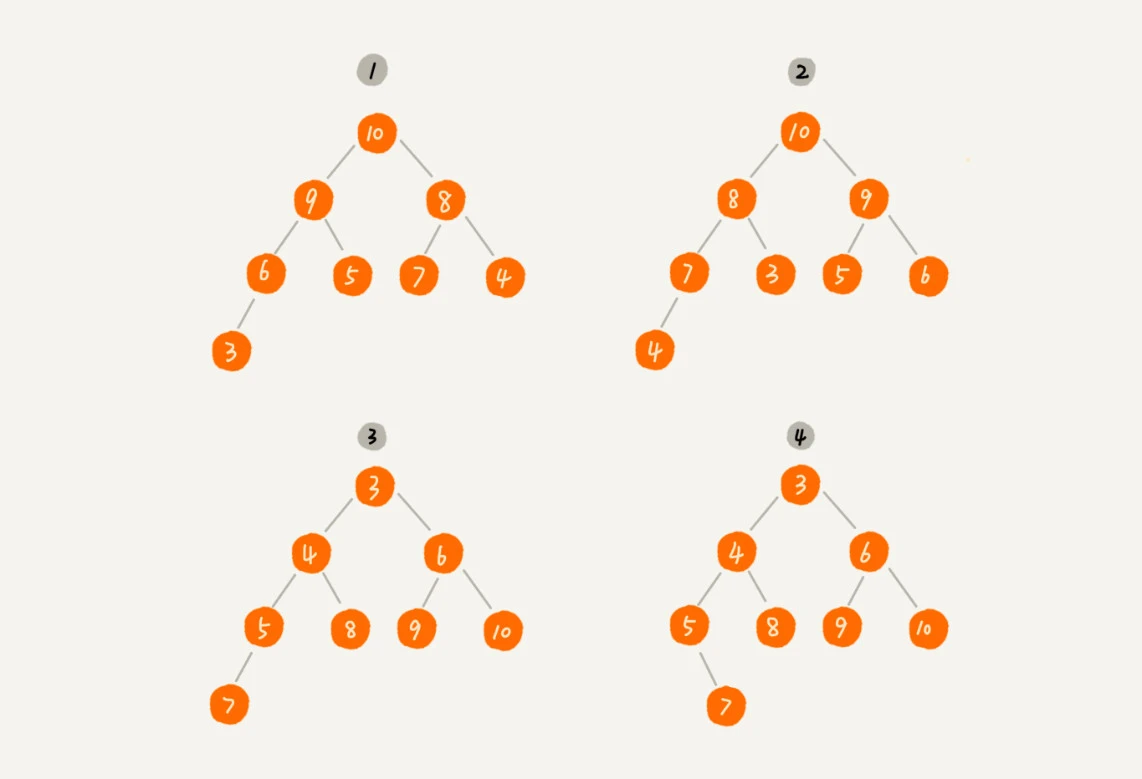
1、2、3 是堆,4 不是堆
如何实现一个堆?
堆是完全二叉树,则非常适合数组来存储,并且还是顺序入值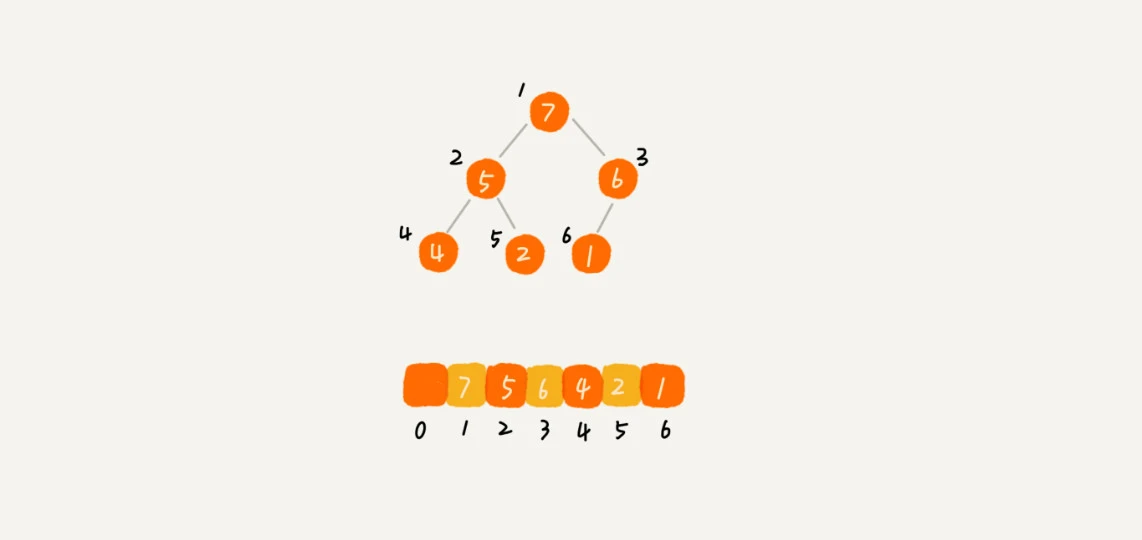
数组中下标为 i 的节点,它的左子节点为 2 i,右子节点为 2 i + 1,父节点为 i / 2
插入元素
插入元素后,还必须满足堆的两个特性。若不满足则进行调整(堆化)
堆化:顺着节点所在的路径,向上或者向下,对比然后交换。分为从下到上、从上到下
大顶堆:根元素最大,然后从大到小
小顶堆:根元素最小,然后从小到大
从下到上堆化
举例:大顶堆,插入 22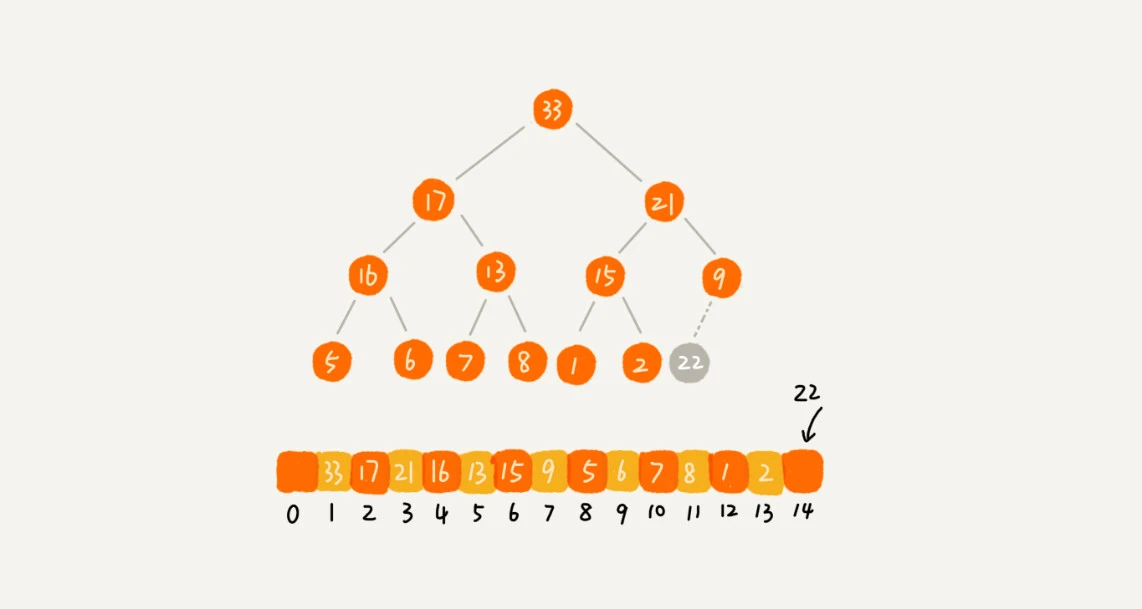
1、22 只能插入到 9 的左节点,满足【特性 1:完全二叉树】
2、开始堆化,先与父节点对比,若父节点大于插入值,是则完成堆化,否则互换
3、继续【步骤 2】,直至满足【特性 2:父节点的值必须大于等于其左右节点的值】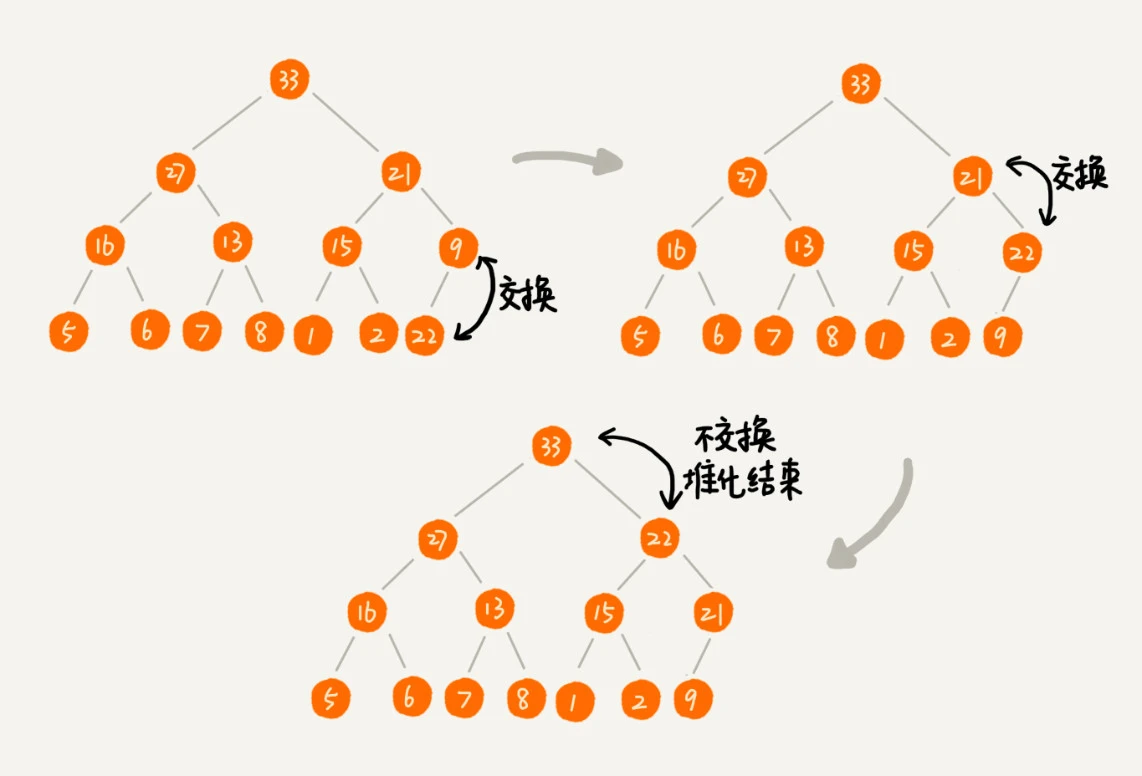
1 | |
删除堆顶元素
当删除堆顶元素后,需要去找第二大或第二小的值作为新堆顶,为了满足【特性 2:父节点的值必须大于等于/小于等于其左右节点的值】
所以删除堆顶元素后,需要递归去处理。那就可以借用从上到下的堆化。
从上到下的堆化:删除堆顶元素后(数组第一个),将最后的元素变为堆顶,然后从上到下进行判断,
解答思考
内容总结
新的思考
27、堆
https://mrhzq.github.io/职业上一二事/算法学习/极客-数据结构与算法之美/数据结构/27、堆/