24、二叉树基础（下）

思考：既然有了高效的散列表，那使用二叉树的地方是不是都可以替换成散列表呢？有没有哪些地方是散列表做不了，必须要用二叉树来做的呢？

主要内容

二叉查找(搜索)树

定义：树中的任意节点，其左子树每个节点的值要小于该节点，而右子树每个节点的值要大于该节点

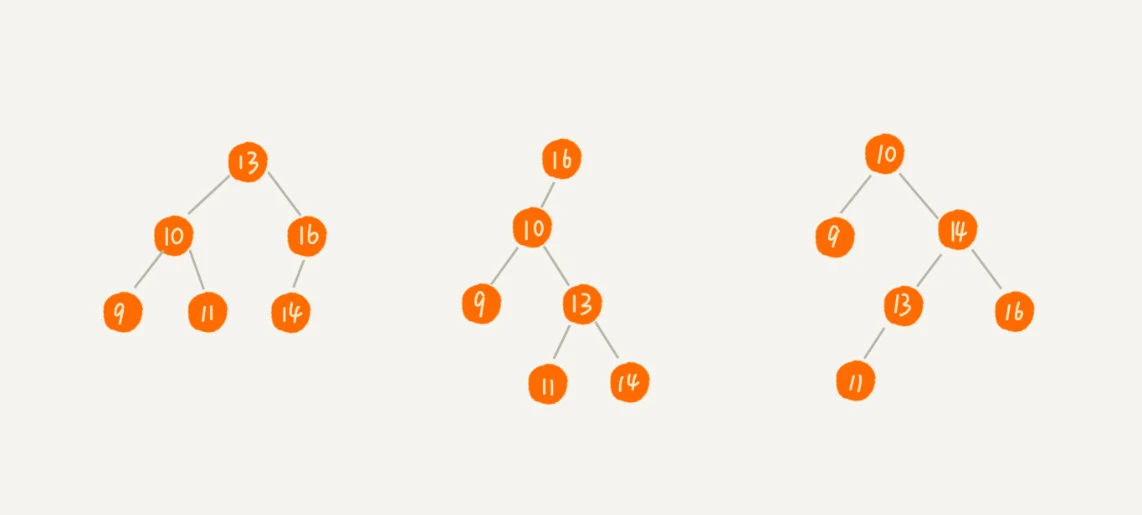
特性：支持动态数据的快速查找、插入、删除操作

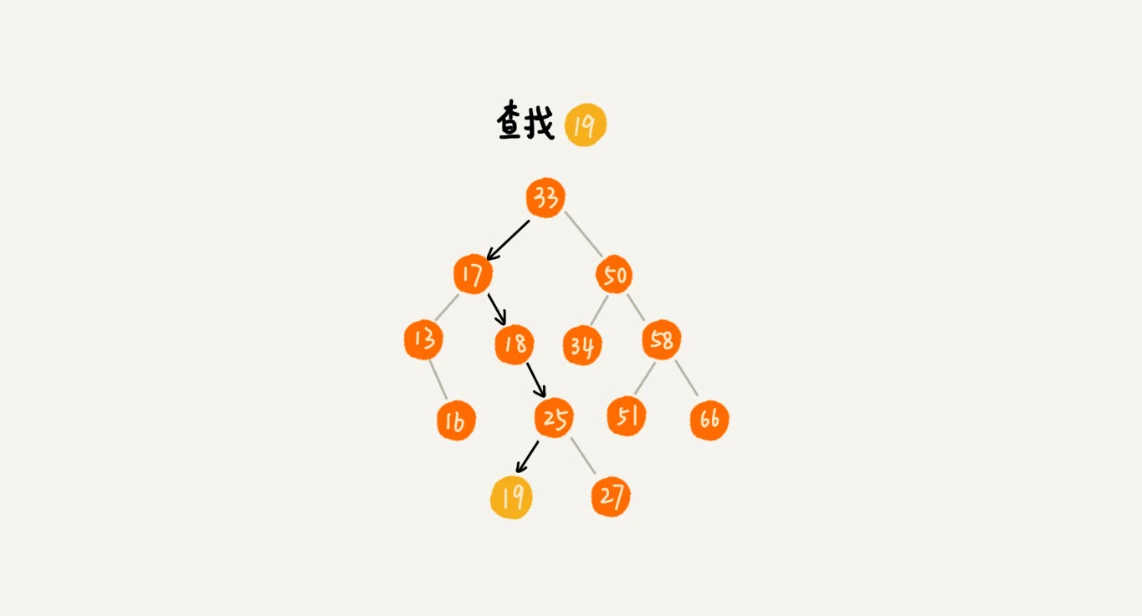
查找操作

查找逻辑：查找值与根节点，若等于则返回，若小于则在左子树中递归找，否则在右子树中递归找

function searchTree(root, targetValue) {
  let p = root

  while(p) {
    if(targetValue > p.value) p = p.right
    else if(targetValue < p.value) p = p.left
    else return p
  }

  return null
}

时间复杂度：最好 O(1)，最坏 O(n)，平均 O(logn)

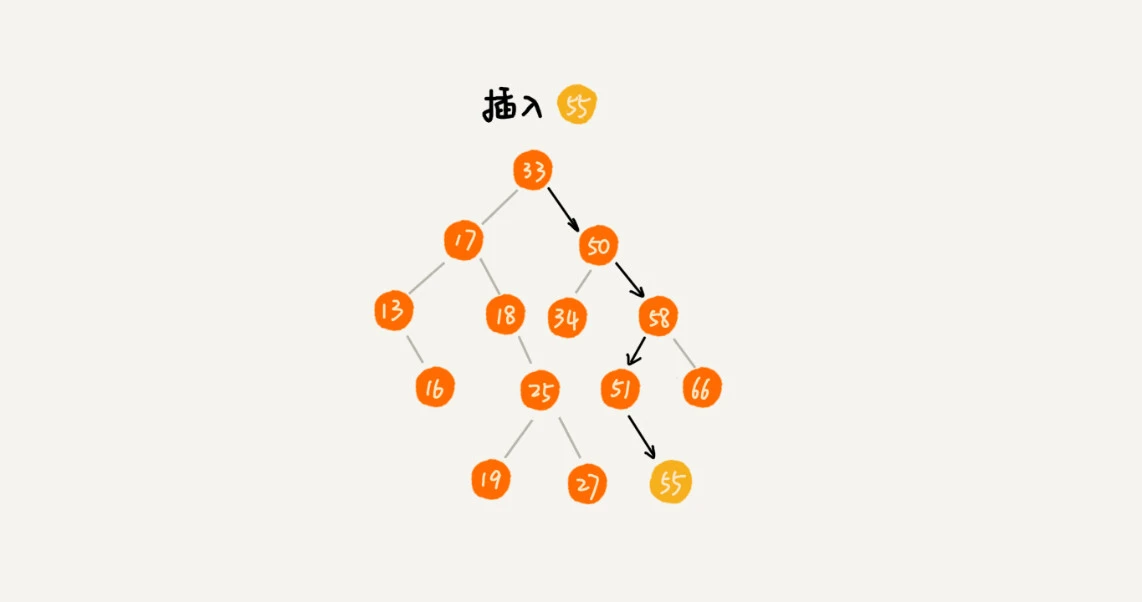
插入操作

新插入的数据一般都是在叶子节点上，所以从根节点开始比较，找到插入位置。
如果插入数据比节点大，若节点的右子树为空则插入，否则再递归遍历右子树，继续找：【如果插入数据比节点大，若节点的右子树为空则插入】
如果插入数据比节点小，若节点的左子树为空则插入，否则再递归遍历左子树，继续找：【如果插入数据比节点小，若节点的左子树为空则插入，否则再递归遍历左子树】

function insertTree(root, targetValue) {
  let p = root

  while(p) {
    if(targetValue > p.value) {
      if(p.right === null) {
        p.right = targetValue
        return
      }
      p = p.right
    }
    else if(targetValue < p.value){
      if(p.left === null) {
        p.left = targetValue
        return
      }
      p = p.left
    }
  }
}

时间复杂度：最好 O(1)，最坏 O(n)，平均 O(logn)

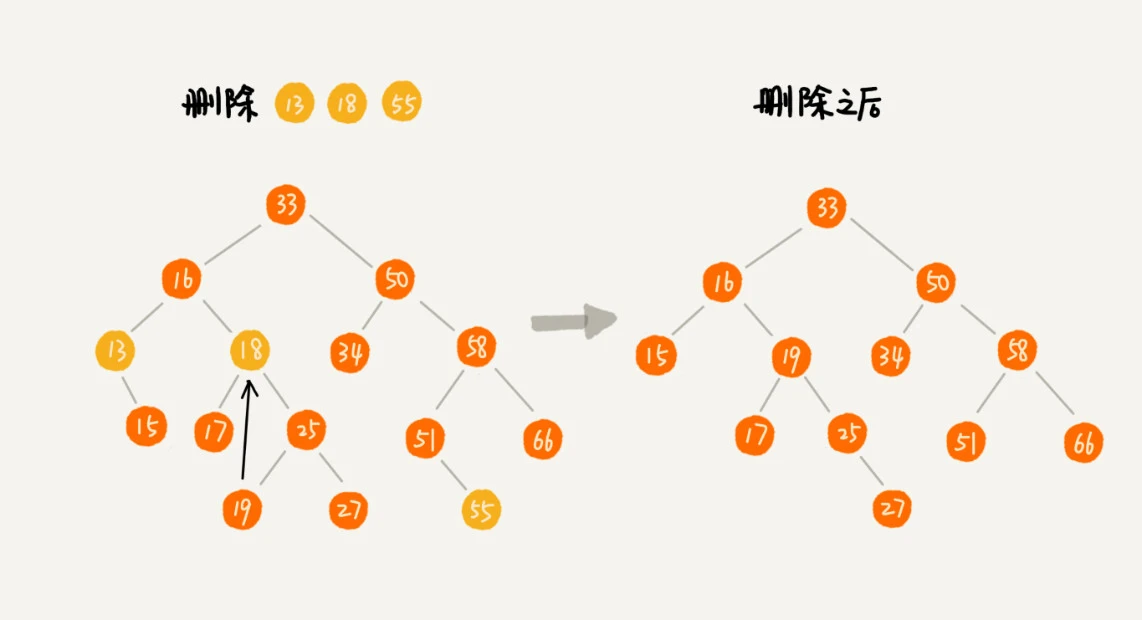
删除操作

三种情况：
1、若删除的节点，无子节点，则直接将父节点的指针改为 null，完成删除；比如下图删除 55
2、若删除的节点，有一个子节点(左或右)，则直接将父节点的指针指向子节点，完成删除；比如下图删除 13
3、若删除的节点，有两个子节点，则先在右子树中找到最小的值，然后和该节点互换，之后再按照【1、2】情况删除该节点；比如下图删除 18

function deleteTree(root, tragetValue) {
  let p = root // 当前节点
  let pp = null // 父节点

  while(p) {
    if(targetValue === p.value) {
      // 相等，结束循环
      return p
    } else {
      // 不相等
      pp = p
      if(targetValue > p.value) p = p.right
      else p = p.left
    }
  }

  // 有两个节点时，删除前的处理
  if(p.right && p.left) {
    let minp = p.right // 右子树最小节点
    let minpp = null // 右子树最小节点的父节点
    while(minp.left) {
      minpp = minp
      minp = minp.left
    }

    p.data = minp.data // 数据替换
    p = minp
    pp = minpp
  }

  let child

  if(p.right) child = p.right // 仅有右节点
  else if(p.left) child = p.left // 仅有左节点
  else child = null // 无子节点

  // 删除节点操作
  if(pp === null) p = child // 删除根节点
  else if(pp.left === p) pp.left = child // 当前 p 属于左节点，则其父级(pp) 的左节点指向 p 的子节点
  else pp.right = child // 当前 p 属于右节点，则其父级(pp) 的右节点指向 p 的子节点
}

时间复杂度：最好 O(1)，最坏 O(n)，平均 O(logn)

解答思考

思考：既然有了高效的散列表，那使用二叉树的地方是不是都可以替换成散列表呢？有没有哪些地方是散列表做不了，必须要用二叉树来做的呢？

内容总结

二叉查找树：结构为 左子节点 < 节点 < 右子节点
其操作的时间复杂度跟树高度成正比，最坏为 O(n)，平均为 O(logn)

新的思考

求一棵给定二叉树的高度？

根节点高度 = 根节点到叶子节点的最大边数
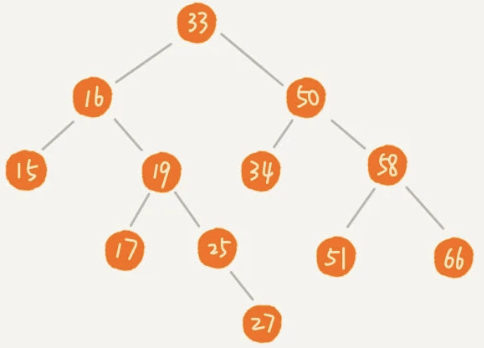高度为：4

// 深度优先遍历：求高度
function heightOfBinaryTree(root, type = "tree") {
  if (root === null) return 0; // 空树的高度为0

  // 递归计算左子树和右子树的高度
  let leftHeight = heightOfBinaryTree(root.left, "left");
  let rightHeight = heightOfBinaryTree(root.right, "right");

  // 返回当前子树（以root为根节点的子树）的最大高度 + 1
  const height = Math.max(leftHeight, rightHeight) + 1;

  return height;
}

// 定义一个二叉树节点结构
function TreeNode(val, left = null, right = null) {
  this.val = val === undefined ? 0 : val;
  this.left = left === undefined ? null : left;
  this.right = right === undefined ? null : right;
}
// 示例用法：
const tree = new TreeNode(
  1,
  new TreeNode(2, new TreeNode(4), new TreeNode(5)),
  new TreeNode(3)
);
console.log(heightOfBinaryTree(tree)); // 输出：3