11、排序(上)
思考:为什么插入排序比冒泡排序更受欢迎?
插入排序和冒泡排序的时间复杂度相同,都是 O(n^2),在实际的软件开发里,为什么我们更倾向于使用插入排序算法而不是冒泡排序算法呢?
主要内容
如何分析一个“排序算法”?
执行效率分析
从以下几个方面进行分析:
- 最好、最坏、平均时间复杂度
- 时间复杂度的系数、常数、低阶
- 针对排序算法,需要去考虑这些
- 比较次数和交换(移动)次数
内存消耗分析
可以使用空间复杂度来衡量
在排序算法中有个“原地排序”算法,特指空间复杂度为 O(1) 的排序算法
稳定性分析
针对序列中的相同值的元素,若排序后,这些值的先后顺序不变,则算为稳定。
举例:2,3,4,6,8,3,9;升序算法后为 2,3,3,4,6,8,9
其中的 3,3,如果它俩的前后顺序未变,则是稳定的排序算法。
冒泡排序
定义:只会操作相邻的两个数,对这两数进行比较,不满足要求则互换。一次冒泡至少会让一个数据移动到它所在的位置,重复 n 次则完成 n 个数据的排序。
比如:4,5,6,3,2,1 进行升序操作
第一次冒泡后数据为:4,5,3,2,1,6,其中 6 已经到达正确位置
一次冒泡的详细比较为:n[0]>n[1] ? 互换 : 不变;n[1]>n[2] ? 互换 : 不变;……;n[4]>n[5] ? 互换 : 不变;
使用 冒泡排序 手写实现 4,5,6,3,2,1 的升序
1 | |
问题:
- 冒泡排序是原地排序吗?
- 是,因为它只涉及到相邻两数的交换,多了个常量级的临时存储空间,所以空间复杂度为 O(1)
- 冒泡排序是稳定的排序算法吗?
- 是,当元素大小相同时,可以不做交换
- 冒泡排序的时间复杂度是多少?
- 最好情况:已排好的数据,只需要一次冒泡操作(因为需要冒泡一下看看是否需要排序),所以为 O(n)
- 最怀情况:反序的数据,则需要 n 次冒泡,则为 O(n^2)
- 平均情况:一般为最坏情况,为 O(n^2)
插入排序
核心思想是取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。初始已排序只有一个元素(数组第一个)
核心操作:对比与移动。
当需要插入 a 时,需要将 a 依次与已排序的元素对比大小(倒着对比),找到插入点。找到插入点后先将插入到后面的元素后移一位,然后再插入。
使用 插入排序 手写实现 4,5,6,3,2,1 的升序
1 | |
问题:
- 插入排序是原地排序吗?
- 是,因为它不需要额外的存储空间,所以空间复杂度为 O(1)
- 插入排序是稳定的排序算法吗?
- 可以处理为稳定排序
- 插入排序的时间复杂度是多少?
- 最好情况:已排好的数据,不需要移动数据,如果从尾到头查找插入点,则为 O(n)
- 最怀情况:反序的数据,则需要 n 次查找,则为 O(n^2)
- 平均情况:一般为最坏情况,为 O(n^2)
选择排序
类似于插入排序,分为两个区,只是每次从未排序区里面取出最小值放入已排序区的末尾。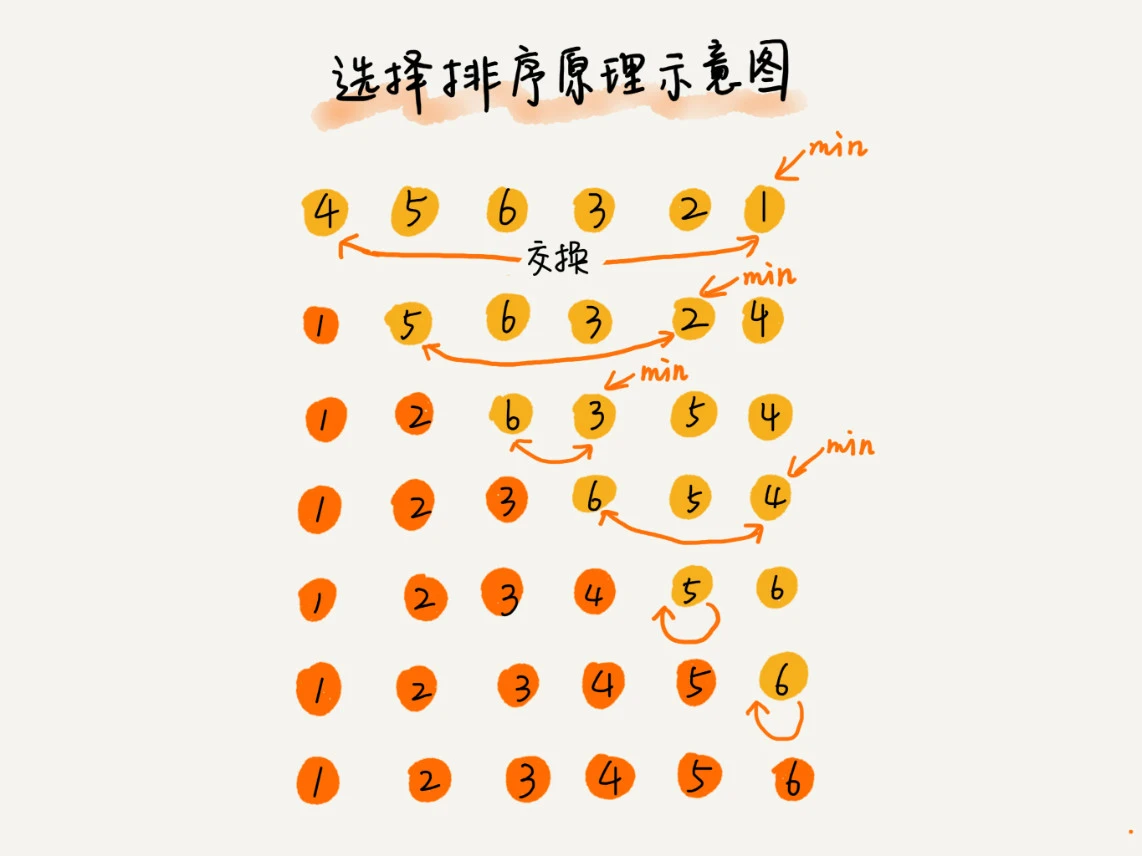
使用 选择排序 手写实现 4,5,6,3,2,1 的升序
1 | |
问题:
- 插入排序是原地排序吗?
- 是,因为它不需要额外的存储空间,所以空间复杂度为 O(1)
- 插入排序是稳定的排序算法吗?
- 不稳定,因为每次选择最小值时拿的是最后的那位(相同数值),然后先插入,这破坏了稳定性。也有可能是和最小值互换,也被破坏了顺序
- 举例:
- 5,4,3’,6,3’’;第一次最小值为 3’’,与 5 互换再插入;第二次最小值为 3’,与 4 互换再插入
- 6’,7,3,6’’,8;第一次最小值为 3,与 6’ 互换再插入;第二次最小值为 6’’,与 7 互换再插入
- 插入排序的时间复杂度是多少?
- 最好情况:已排好的数据,不需要交换数据,但都每次需要找最小,所以为 O(n^2)
- 最怀情况:反序的数据,则需要 n 次对比,则为 O(n^2)
- 平均情况:一般为最坏情况,为 O(n^2)
解答思考
思考:为什么插入排序比冒泡排序更受欢迎?
插入排序和冒泡排序的时间复杂度相同,都是 O(n^2),在实际的软件开发里,为什么我们更倾向于使用插入排序算法而不是冒泡排序算法呢?
因为它们两个的移动/交换代码复杂度不同
1 | |
假设每行代码执行时间相同,为 T。
那冒泡交换逻辑为 3 T,插入移动逻辑为 1 T
那面临大规模数据时,之间的差异将更大
所以为了追求性能,尽管它们的时间复杂度都为 O(n^2),但还是优先选择插入排序
总结
冒泡:核心是相邻两数对比与交换
插入:核心是未排序元素依次与已排序元素(倒着)对比找到插入点然后插入,会涉及一些元素的移动
选择:核心是找到未排序元素最值(小或大),插入已排序元素最末尾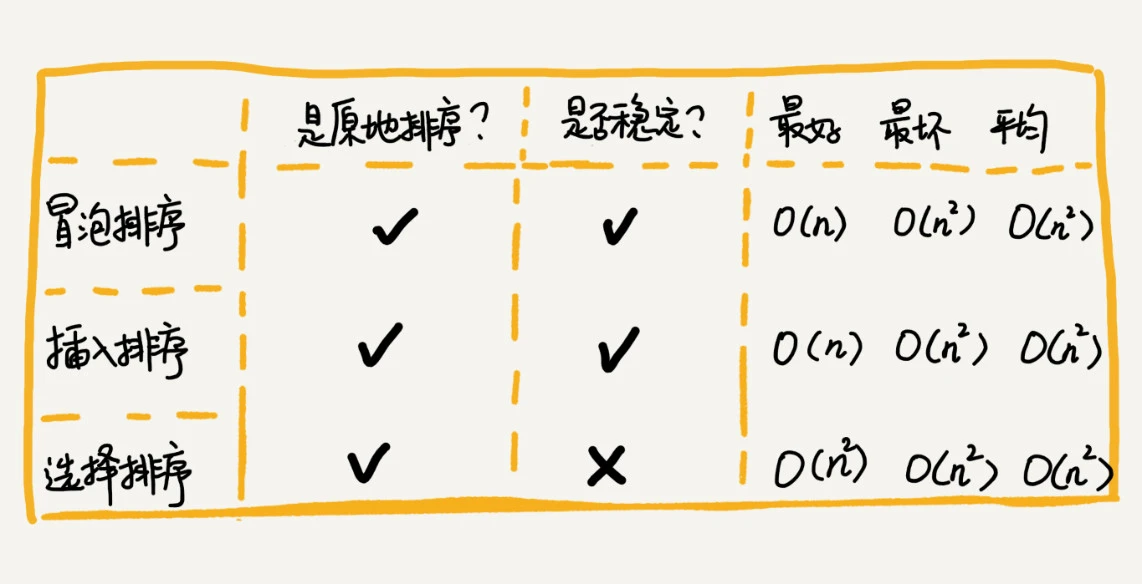
这三个的时间复杂度太高,只适合小规模数据,在实际开发中应用并不多,学习它们也只是为了开拓思维。
新的思考
如果这三个的数据是存储在链表中,这三种排序算法还能工作吗?如果能,那相应的时间、空间复杂度又是多少呢?
冒泡:可以,交换时改变指向,代码写的更复杂
插入:可以,插入时直接改变指针
选择:可以,交换时要改变指向,代码写的更复杂,插入时也要处理好指向
然后时间、空间复杂度都未发生变化。