10、递归

思考：如何用三行代码找到“最终推荐人”？
比如：用户 A 推荐用户 B 来注册，用户 B 又推荐了用户 C 来注册。则用户 C 的“最终推荐人”为用户 A，用户 B 的“最终推荐人”也为用户 A，而用户 A 没有“最终推荐人”。
一般，会通过数据库来记录这种推荐关系。在数据库表中，其中 actor_id 表示用户 id，referrer_id 表示推荐人 id。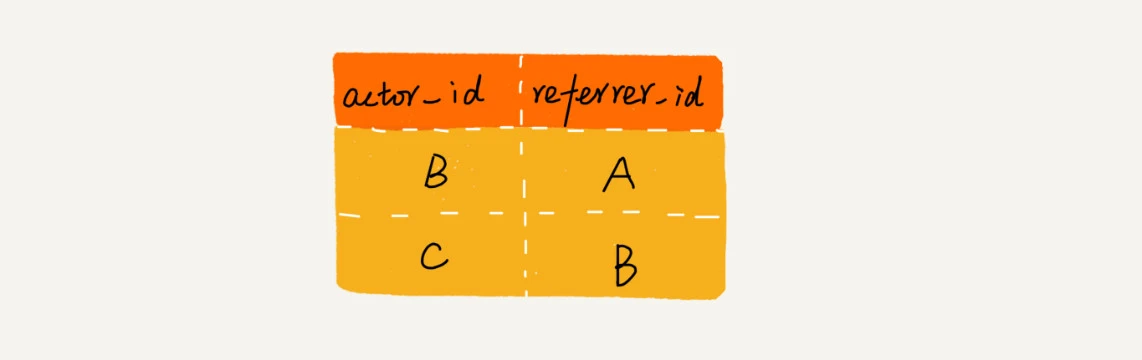

问题：若给定一个用户 ID，如何查找这个用户的“最终推荐人”？

主要内容

递归：函数或方法通过调用自己来解决问题
递：函数调用的过程，归：值返回的过程

// 自然数的递归函数
function f(n) {
  if(n === 1) return 1
  return f(n - 1) + 1
}

递归公式：f(n) = f(n - 1) + 1; 其中终止条件 f(1) = 1

使用递归的三个条件：

1. 【原问题】可以分解为多个【子问题】
   1. 【子问题】指：数据规模更小的问题
2. 要求【子问题】跟【原问题】除数据规模不同，求解思路要一致
3. 必须有终止条件

写递归的关键

先写递推公式，找到终止条件

案例：假如这里有 n 个台阶，每次你可以跨 1 个台阶或者 2 个台阶，请问走完这 n 个台阶有多少种走法？
如果有 7 个台阶，你可以 2，2，2，1 这样子上去，也可以 1，2，1，1，2 这样子上去，总之走法有很多，那如何用编程求得总共有多少种走法呢？

递推公式推导思路：由于限制了每次走的台阶为 1 或 2，则可以分为两类：第一步走了 1 个台阶，求后续 n - 1 的走法；第一步走了 2 个台阶，求后续 n - 2 的走法；
所以递推公式：f(n) = f(n - 1) + f(n - 2)
终止条件推导思路：走 1 个台阶走法为 1，所以终止条件 1 为 f(1) = 1，那 f(2) = f(1) + f(0) 就发现 f(0) 无值，所以 f(0) = 1？发现这不合理，走 0 个台阶有 1 个走法？所以将 f(2) 等于 2，作为终止条件 2。
再测试下 f(3) = f(2) + f(1) = 3， f(4) = f(3) + f(2) = f(2) + f(1) + f(2) = 2+1+2 = 5
所以终止条件：f(1) = 1，f(2) = 2
所以汇总递推公式下：

f(1) = 1
f(2) = 2
f(n) = f(n - 1) + f(n - 2)

对应的递归代码为：

function f(n) {
  if(n === 1) return 1
  if(n === 2) return 2
  return f(n -1) + f(n -2)
}

总结：写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。

警惕堆栈溢出

为什么会溢出呢？

因为函数调用时会将临时变量入栈，但系统分配的栈的大小一般有限，所以在递归大规模数据时容易一直入栈，就有溢出风险。
比如上面求走台阶法的，如果在 JS 中执行f(9999)，就会报错：Uncaught RangeError: Maximum call stack size exceeded，在执行f(999)时就会卡死了

那如何避免呢？

简单操作：可以设置最大调用深度，当超过后就直接报错

const maxDeep = 1000
let deep = 1

function f(n) {
  ++deep

  if(deep >= maxDeep) throw new Error('超出最大调用次数')

  if(n === 1) return 1
  if(n === 2) return 2
  return f(n -1) + f(n -2)
}

警惕重复计算

什么是重复计算？

还是上面那个求走台阶法，以下是求 f(6) 的步骤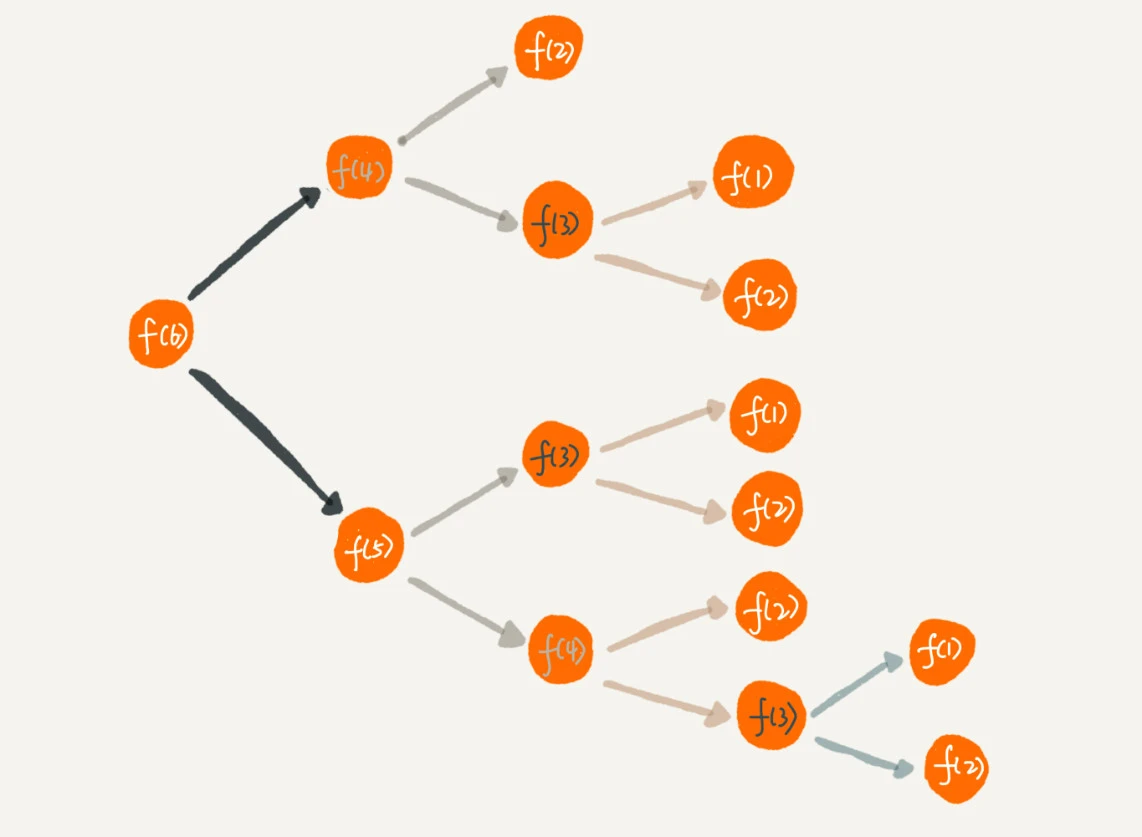

可以发现 f(4)、f(3) 都出现了多次，这就是重复计算

那如何避免呢？

可以使用另一个数据，来存储已经计算过的值，每次使用前判断是否存在，有的话直接取

const fMap = new Map()

function f(n) {
  if(n === 1) return 1
  if(n === 2) return 2

  if(fMap.get(n)) {
    return fMap.get(n)
  }

  const tmp = f(n -1) + f(n -2)

  fMap.set(n, tmp)

  return tmp
}

// 执行 f(6) 后
// fMap 为 Map(4) {3 => 3, 4 => 5, 5 => 8, 6 => 13}

其他问题

由于递归调用函数，所以当数据规模大时，递归的时间复杂度就不可预测，对应空间复杂度也要考虑每次调用函数时的入栈所占用的开销

如何将递归改为非递归

由于递归的堆栈溢出、重复计算、不可控的时间/空间复杂度等问题，所以实际开发中视情况使用递归。
将上述的求台阶走法改为非递归

function f(n) {
  if(n === 1) return 1
  if(n === 2) return 2

  let res = 0
  let pre = 2 // 对应 f(2)
  let prepre = 1 // 对应 f(1)

  for(let i = 3;i <= n; i++) {
    res = pre + prepre
    prepre = pre
    pre = res
  }

  return res
}

解答思考

思考：如何用三行代码找到“最终推荐人”？
递推公式：f(id) = f(r_id)
终止条件：f(1) = null

function getReferrerId(actorId) {
  // 接口获取该用户 id 的推荐人 id
  const referrerId = axios.getReferrerId({ actorId })
  if(referrerId === null) return referrerId
  return getReferrerId(referrerId)
}

新的思考

平时调试代码会使用 IDE 的单步跟踪功能，像规模比较大、递归层次很深的递归代码，几乎无法使用这种调试方式。对于递归代码，有什么好的调试方法呢？

1.打印日志发现，递归值。
2.结合条件断点进行调试。